Die Formel für das Volumen einer sechseckigen Pyramide: ein Beispiel zur Lösung des Problems
Die Berechnung von Volumina räumlicher Figuren ist eine der wichtigen Aufgaben der Stereometrie. In diesem Artikel werden wir die Frage der Bestimmung des Volumens eines solchen Polyeders als Pyramide betrachten und auch ein sechseckiges regelmäßiges geben.
Sechseckige Pyramide
Betrachten wir zunächst, worum es in der Figur geht, die in dem Artikel besprochen wird.
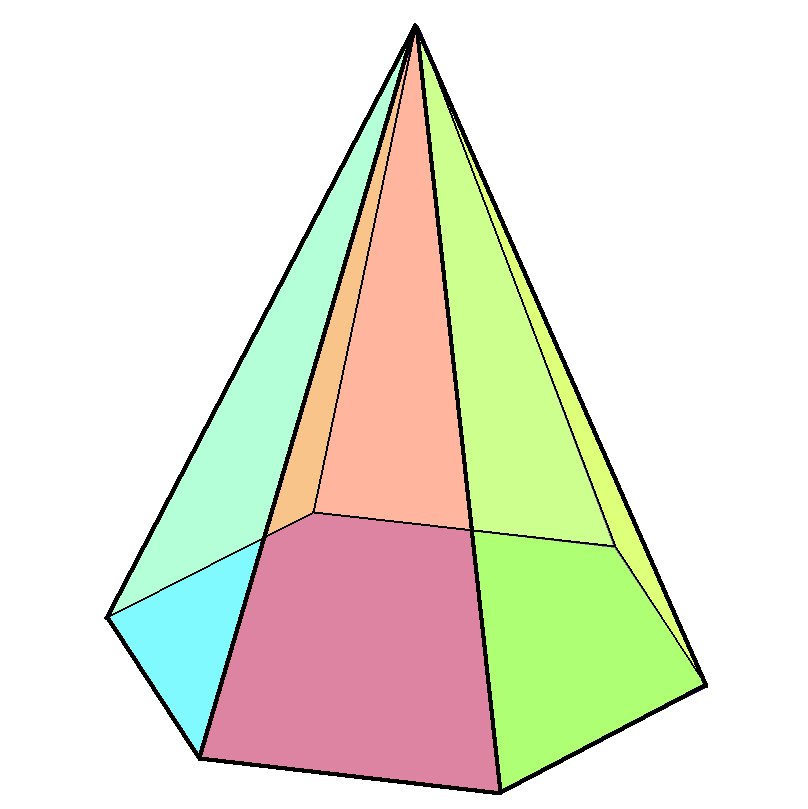
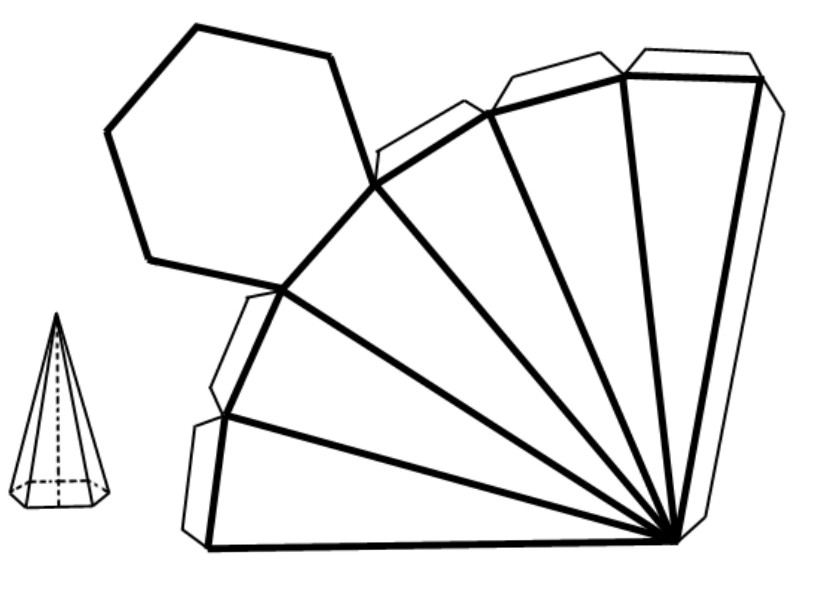
Angenommen, wir haben ein beliebiges Sechseck, dessen Seiten nicht unbedingt gleich sind. Nehmen wir außerdem an, dass wir einen Punkt im Raum ausgewählt haben, der nicht in der Ebene des Sechsecks liegt. Indem wir alle Ecken des letzteren mit dem ausgewählten Punkt verbinden, erhalten wir eine Pyramide. In der Abbildung unten sind zwei verschiedene Pyramiden mit sechseckiger Grundfläche dargestellt.
Es ist zu erkennen, dass die Figur neben dem Sechseck aus sechs Dreiecken besteht, deren Verbindungspunkt als Scheitelpunkt bezeichnet wird. Der Unterschied zwischen den gezeigten Pyramiden besteht darin, dass die Höhe h der rechten die sechseckige Grundfläche nicht in ihrem geometrischen Zentrum schneidet, sondern die Höhe der linken Figur genau in diese Mitte fällt. Dank dieses Kriteriums wurde die linke Pyramide als gerade und die rechte als geneigt bezeichnet.
Da die Basis der linken Figur in der Figur von einem Sechseck mit gleichen Seiten und Winkeln gebildet wird, wird sie als regelmäßig bezeichnet. Im weiteren Verlauf des Artikels werden wir nur über diese Pyramide sprechen.
Um das Volumen einer beliebigen Pyramide zu berechnen, gilt folgende Formel:
Dabei ist h die Länge der Höhe der Figur, S o die Fläche ihrer Basis. Verwenden wir diesen Ausdruck, um das Volumen einer regelmäßigen sechseckigen Pyramide zu bestimmen.
Da an der Basis der betrachteten Figur ein gleichseitiges Sechseck liegt, lässt sich dessen Fläche mit dem folgenden allgemeinen Ausdruck für ein n-Eck berechnen:
S n = n / 4 * a 2 * ctg (pi / n)
Dabei ist n eine ganze Zahl gleich der Anzahl der Seiten (Ecken) des Polygons, a ist die Länge seiner Seite, die Kotangensfunktion wird mit den entsprechenden Tabellen berechnet.
Wenden wir den Ausdruck für n = 6 an, erhalten wir:
S 6 = 6/4 * a 2 * ctg (pi / 6) = √3 / 2 * a 2
Nun bleibt noch dieser Ausdruck in die allgemeine Formel für das Volumen V einzusetzen:
V 6 = S 6 * h = √3 / 2 * h * a 2
Um das Volumen der betrachteten Pyramide zu berechnen, ist es daher notwendig, ihre beiden linearen Parameter zu kennen: die Länge der Seite der Basis und die Höhe der Figur.
Ein Beispiel für die Lösung des Problems
Lassen Sie uns zeigen, wie der erhaltene Ausdruck für V 6 verwendet werden kann, um das folgende Problem zu lösen.
Das richtige Volumen beträgt bekanntlich 100 cm 3. Es ist notwendig, die Seite der Basis und die Höhe der Figur zu bestimmen, wenn bekannt ist, dass sie durch die folgende Gleichheit zueinander in Beziehung stehen:
Da die Volumenformel nur a und h enthält, ist es möglich, jeden dieser Parameter, ausgedrückt durch den anderen, darin zu ersetzen. Ersetzen Sie beispielsweise a, erhalten wir:
V 6 = √3 / 2 * h * (2 * h) 2 =>
h = ∛ (V 6 / (2 * √3))
Um den Wert der Höhe der Figur zu ermitteln, müssen Sie die dritte Wurzel des Volumens ziehen, die der Abmessung der Länge entspricht. Wir ersetzen den Wert des Volumens V 6 der Pyramide aus der Bedingung des Problems, wir erhalten die Höhe:
h = ∛ (100 / (2 * √3)) ≈ 3,0676 cm
Da die Seite der Basis entsprechend der Problemstellung doppelt so groß ist wie der gefundene Wert, erhalten wir den Wert dafür:
a = 2 * h = 2 * 3,0676 = 6,1352 cm
Das Volumen einer sechseckigen Pyramide lässt sich nicht nur durch die Höhe der Figur und den Seitenwert ihrer Grundfläche ermitteln. Es reicht aus, zwei verschiedene lineare Parameter der Pyramide zu kennen, um sie zu berechnen, zum Beispiel Apotem und die Länge der Seitenrippe.